Goidna Schnidd
| Der Artikl is im Dialekt Westmittlboarisch gschriem worn. |
Da Goidne Schnidd (lat. sectio aurea, dt. Goldener Schnitt, engl. golden ratio) is as Vahejtnis zwischn zwoa Zoin vo grob 1:1,618. In da Kunst, im Design und in da Architektua werd des oft aa ois de ideale Proportion vo zwoaraloa Länga zuaranand ogseng und guit ois da Inbegriff vo Esthetik und Harmonie. Mehra no gibts des Vahejtnis vom goidnan Schnitt aa in da Natua, wora se duach mehrane intressante mathematische Meakmoi auszoachna duad. Gnennd weada aa stetige Teilung und geddliche Teilung (lat. proportio divina).

Definitiona und Grundmeakmoi[Werkeln | Am Gwëntext werkeln]
- Zwoa Streckn stengan im Vahejtnis vom Goidnen Schnitt, wenn se d´greßane zua gleana vahoit wiad Summ aus boadn zua greßan (schaug Buidl). Des Vahejdnis werd vui midm griachischn Buachstom Φ (Phi) ausgschuidad. Wenn iatzad d längane Streck a und d kiazane b is, nachad guit
- Oiso hamma firas Vahejdnis vo a zu b (schaug obi)
- Φ is a irrationale Zoi, des hoaßt, dass a se niat duach a Vahejdnis vo zwoaraloa ganze Zoin dorstejn losst. Es zoagt se, dass s in am gwissn Sinn de irrationaiste vo olle Zoin is (schaug obi). Des bedeit, dass sa se aa no vagleichsweis schlecht duach a Vahejdnis vo zwoa ganze Zoin onahan loßt, a Zuastand, dea wo wesentli zua iara Bedeitung in da Natua und woahrscheins aa in da Kunst beitrogt.
- Subtrahiat ma de kiazane vo de zwoa Streckn vo da längan, so kriagt ma a no kiazanane Streckn, zua dea de mittlane vo drei Streckn aa wiada im Vahejdnis vom Goidnan Schnitt stähd. Des kriagma aus dera Definition vo om, wemma vo da Streckn a+b de Streckn b obziagt. De Bezeichnung stetige Teilung hoaßt dabei sofui wia, dass se der Vorgang grod beliebig oft wiadahoin loßd und nachad oiwei wiada as sejba Vahejdnis liafad.
- A Rechteck, des wo an Seitenvahejdnis im Goidnan Schnitt hod, hoaßt ma as Goidne Rechteck und es wern aa gleichschenklige Dreieck Goidne Dreieck gnennt, wann bei dene zwoa Seitn in dem Vahejdnis stenga duan.

- A bedeitnde Roin spuid da sognennde Goidne Winkl Ψ (Psi). Ma kriagt eam, wemma an Winke 360° im Vahejdnis vom Goidnan Schnitt teit. Bezeichnet ma an kleanan vo de zwoa Winkl ois Ψ1 und an ßan mit Ψ2, so ergibt se
- Wei se Winkl kleana wia 180° fiad Owendung ois handlicha daweisn, werd da kleana Winkl Ψ1 Goidna Winkl Ψ gnennt, oiso
- In am enga Zammadhang zum Goidnan Schnitt stähd de unendliche Zoinfoige vo de Fibonacci-Zoin, de wo aufn Leonardo da Pisa, gnennd Fibonacci (13. Joarhundat), zruckegähd:
- für und ois Ofangswerte und
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946
- Aa d jeweis naxte Zoi in dera Foign dahoit ma oisd Summe vo de zwoa voaheagangana. As Vahejdnis vo zwoa nacharanandkemmadn Fibonacci-Zoin gähd fia unendlich gegan Goidnan Schnitt, wos da Johannes Kepler seinazeit aa scho gwisst hod.
Geometrischs[Werkeln | Am Gwëntext werkeln]
Vagleich mid ondane Teilungsvahejdnissn[Werkeln | Am Gwëntext werkeln]
A Grund fiad Beliabtheit vom Goidnan Schnitt kunnt sei hoha Grad an Irrationalität sei. Des bedeit, dassa se vo olle Vahejdniss zwischn gleanare ganze Zoin, wia 2 : 3 oder 3 : 4, deitlich obhehm duad, wos in am bestimmtn ästhetischen Zammadhang dawinscht sei konn. Kunnt sei, er warad und werd aa vui unbewusst und ohne gscheide Maßkontroin intuitiv gwejhd, um sejchane rationale Längenvahejdniss zum vermeihn.
D´foignde Obbildung vagleicht vaschiadne Rechtecke mid schneidige Seitnvahejtniss in da Umgebung vo Φ. Ogehm werd oiwei as Vahejdnis vo da He zua Broadn und am entsprechadn Zoinfaktor.
Typische Einsotzgebiet (vo links auf rechts):
- 4 : 3 – Traditionejs Fernsehformat. In da Regl aa bei Computermonitoren (z. B. 1024 × 768 Pixel). Des Format gähd zruck auf Thomas Alva Edison, dea wo 1889 as Format vom klassischn Fuimbuidl (35-mm-Film) auf 24 × 18 mm festglegt hod.
- √2 : 1 – As Seitnvahejdnis beim DIN-A4-Bladdl und de vawandtn DIN-Maßn. Bei a Hoibiarung durch an Schnitt, dea wos de längane Seitn vom Rechteck hoibiat, entstengan wiada Rechteck mit am sejbn Vahejdnis.
- 3 : 2 – Seitnvahejdnis beim Kloabuidfuim (36 mm × 24 mm).
- Φ : 1 – Seitnvahejdnis im Goidnen Schnitt. Do approximiat, oiso ognähat, duach 144 × 89 Pixel mid am theoretischn Fejla vo nur 5·10−5. De zwoa benachbarten Rechteck (3 : 2 und 5 : 3) ham Seitnvahejdniss vo aufanandafoignde Fibonacci-Zoin und approximieren desweng aa an Goidnen Schnitt vagleichsweise guad.
- 5 : 3 – Findt nehm am no breadan 1 : 1,85 ois Kinoformat Vawendung.
- 16 : 9 – Broadbuidfernseha.
Konstruktiona mim Ziakl und Lineai[Werkeln | Am Gwëntext werkeln]
In da Geometrie gibts Konstruktionsvafoarn fian Goidnan Schnidd, de wo nur mid Ziakl und Lineai auskemman. Fiah´d Teilung vo ana Streck im Vahejdnis vom Goidnan Schnitt gibts recht vui sejchana Vafoarn. Es weand expemplarisch a boar gnennt.

|

Bei dene zwoa Beispui redt ma aa vo na innan Teilung vo da Ausgangsstreckn AB. |

|

|
Druhnfuaß (Pentagramm)[Werkeln | Am Gwëntext werkeln]


As Pentagramm, oans vo des ejdastn magischen Symbole vo da Kuituagschicht, stähd in a bsundas enga Beziahung zum Goidnan Schnidd.
Zu a jäda Streckn und Teistreckn findt se as Gegnstick, des wo mit eahm im Vahejdnis vom Goidnan Schnidd stähd. In da Obbildung han olle drei mögliche Strecknpaare in a blaun Fob (längerne Streckn) und in a orangna Fob (kiazaneh Streckn) markiert. Übas oben gschrimne Vafoarn vo da 'stetigen Teilung loß´nahse nacharanand erzeugn. Theoretisch kannt mas im vakleanadn Druhnfuaß fortsetzn, wos ma ins innerne Fünfeck zeichnen kannt, und so aa in olle weídahn. Standn de zwoa Streckn im Vahejdnis vo ganze Zoin, miassad des Vafoarn vo da furthgsetztn Subtraktion na amoi Null ergehm und obbrecha. D´Betrachtung vom Druhnfuaß zoagt aba guad, dass´ iat da Foi is.
Fiahn Beweis, dass aa a Goidner Schnitt is, muaß ma seng, dass neba de Streckn, de olle aus Symmetriegründ gleich long sandt, aa CD=CC' guit. Des kimmd daher, dass as Dreieck DCC' zwoa gleiche Winkl hod, wia ma beim Parallelvaschiam vo da Streckn CC' sigt, und desweng gleichschenklig is. Nochm Strohlnsotz guit :
Dasetzt ma AC=AB+BC und beacht d´Gleichheit vo de auftredendn Teilstück, so erhoit ma genau d´obige Definitionsgleichung fiahn Goidnen Schnitt.
Goidne Spirale[Werkeln | Am Gwëntext werkeln]

A Goidns Rechteck loßt se in a Quadrat und in no a Goidns Rechteck zerlegn. Durch wiadahoide Teilung erhoit ma a Figur, de se in a logarithmische Spirale eizeichnen loßt. Oft werds aa, wie in dera Obbildung, durch a Foign vo Viertlkreise approximiert. Ihr Radius ändert se bei a jäda 90°-Drehung um den Faktor Φ.
De schnecknförmign Kalkheisl vo a bor Tierartn ham a ähnliche Steigung, wia beispielsweise de vom Nautilus. Bei de meistn vo dene Tierartn iss´d Steigung oba ned so steil.
Goidner Schnitt im Ikosaeder[Werkeln | Am Gwëntext werkeln]

De 12 Eckn vom Ikosaeder buihn d´Eckn vo drei gleich große, senkrecht zuaranand stehende Rechtecke mid am gemeinsamen Mittlpunkt und mit am Seitnvahejdnis im Goidna Schnitt. D´Anordnung vo dene drei Rechtecke hoaßt aa Goidner-Schnitt-Stui.
Historischs[Werkeln | Am Gwëntext werkeln]
Hippasos vo Metapont (um 450 v. Kr.), der am Geheimbund der Pythagoreer oghead hod, is bei seine Studien am Fünfeck oufgfoin, dass as Vahejdnis vo Kontnläng zur Diagonale ned durch ganze Zoin darstellbar war. Des stand im Widerspruch zur Überzeigung vo de Pythagoreer, dass d´Wejd se foiständig durch ganze Zoin bschreim loßn miassad. Ironischerweis homms d´Widerlergung dieser Ansicht agrad in eahne eignen Symbol, dem Druhnfuaß, ghabt. Hippasos hod oiso as Phänomen vo irrationale Zoin anhand da Inkommensurabilität vo Streckn gfundn – dass oiso fiah BC und AD im Buidl vo ohm koa Maß gibt, so dass de zwoa Streckn beide ganzzahlige Vielfache davo wahrn – sowia zwoa Größn, de im Vahejdnis vom Goidnen Schnitt stengand. Unbestätigtn Berichtn zuafoign hodda des oba aa no andane Leid vazejhd und na hammd d´Leid vom Geheimbund eahm zur Strof datränkt.
D´easchte gscheide Beschreibung vom Goidnen Schnitt is vom Euklid (325 – 270 v. Kr.), der auf den bei seine Untersuchungen an de platonischen Körpern – in Seitnflächn zuaranand kongruente regelmäßige Vielecke – und am Fünfeck beziehungsweis am Druhnfuaß draufgstoßn is. Sei Bezeichnung fiah des Teilungsvahejdnis hamms späda ois "proportio habens medium et duo extrema" eideitscht, wos heid "Teilung im inneren und äußeren Vahejdnis" hoaßad"
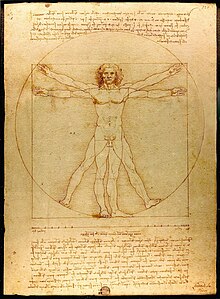
Späda beschäftigte sich da Franziskanermönch Luca Pacioli di Borgo San Sepolcro (1445–1514), der an da Universität vo Perugia in Italien Mathematik glehrt hod, mit Euklids Arbeiten. Er hod d´Streckenteilung Göttliche Teilung gruafa, wos se auf Platons Indentifizierung der Schöpfung mit de fünf platonischen Körpern bezog, zu dera ihra Konstruktion da Goidne Schnitt a wichtigs Huifsmittl dorstejhd. Sei gleichnomigs Werk De Divina Proportione vo 1509 bstähd aus drei unabhängige Biacha. Bei de easchtn handelts se um a rein mathemitsche Obhandlung, die jedoch koanaloa Bezuag zur Kunst und Architektur heaschtejhd. As zwoate is a kurzs Traktat über d´Schriften des Remers Vitruv ausm 1. Jahrhundert v. Kr. zur Architektur, in dene Vitruv – a rämischa Architekt, Ingenieur und Schriftstella – d´Proportionen des menschlichen Körpers ois Vorlage fiah Architektur dorstejhd. Des Biache enthoidt a Studie vo Leonardo da Vinci (1451–1519) übern virtruvischn Menschn. As Vahejdnis da Quadratseitn zum Kreisradius in dem berühmtn Buidl is mit a 1,7%-tigen Abweichung da Goidne Schnitt, der in dem Biacha, des wo dazuaghead, gor ned erwähnt werd. Aa daad ma de Abweichung bei am konstruktiven Verfohrn ned erwartn.
In Obhandlungen vaschiana Autorn im 19. Joarhundert, bsunders vom Philosophen Adolf Zeising (Lit.: Zeising, 1854) san de zwoa Schriftn zua Thesn zamgfügt worn, Pacioli häd in da De Divina Proportione in Zammorbat min Leonardo da Vinci an Zammadhang zwischn Kunst in am Goidnen Schnitt heagstejhd und na sei Wiadaentdeckung fiah´d Molerei vo da Renaissance gründt. Zeising is vo da Existenz von am Naturgsetz da Ästhetik überzeigt gwehn, vom dem d´Basis da Goidne Schnitt häd sei miassn. Er hod gsuacht und aa überroin an Goidnen Schnitt gfundn. Seine Schriftn hom se nachad rasch verbreit und a gscheide Euphorie ausglöst. Ondraseits zaogt a Literatuaanalyse, dass vorm Zeising neamands in de Werke der Antikn oder da Renaissance an Goidnen Schnitt z´kenna glaabt hod. Deraloa Fund´ hand oiso heidzdog umstrittn.
D´Bezeichnung Goidner Schnitt is easchtmois 1835, oiso nur wenige Joar dafiah, vo Martin Ohm (1792–1872; Bruada vo Georg Simon Ohm) in am Lehrbiache da Mathematik verwendt worn (Lit.: Ohm, 1835). Aa des mit dera 'sectio aurea kimmd vo dera Zeit.
Gustav Theodor Fechner, a Begründer da experimentelln Psychologie, hod 1876 bei Untersuchungen mid Versuachspersona anhand vo Rechteck´ agrad a Präferenz fiahn Goidnen Schnitt festgstejhd (Lit.: Fechner, 1876). D´Ergebniss´ der Strecknteilung und bei Ellipsn hand oba andeascht ausgfoin und neizeitliche Untersuchungen zoagn, dass as Ergebnis vo sejchane Experimente stark aa vom Kontext der Dorbietung obhängt. Fechner hod bei Vamessungen vo Buidln in vaschiane Museen Europas aa no gseng, dass d´Seitnvahejdniss im Hochformat im Mittel etwa 4:5 und im Querformat etwa 4:3 btrogn und se damit deitlich vom Goidnen Schnitt unterschein.
Onfang vom 20. Joarhundert warn d´Schriftn vom Rumänen Matila Costiescu Ghyka (1927) zum Goidnen Schnitt aktuell, de wo den religiösen Askept vo Pacioli mihm ästhetischn vo Zeising vabundn hom. Fiah eahm war da Goidne Schnitt as fundamentale Gheimnis des Universums und hod dazu vor ollem Beispui aus da Natur brocht.
Am End´ vom 20. Joarhundert hod d´Kunsthistorikerin Marguerite Neveux mid röntgenanalytische Vafoarn unta da Forb vo Originalgmejdter, de angeblich an Goidnen Schnitt enthoitn, vergeblich noch deraloa Markierungen oder Konstruktionsspuren gsuacht (Lit.: Neveux, 1995).
Architektua[Werkeln | Am Gwëntext werkeln]
Friae Hiiweis aufd vermuatlich unbewusste Vawendung vom Goidnan Schnidd hand aus da Architektua bekonnt. D´Schriften vom griachischn Gschichtsschreiba Herodot zua Cheops-Pyramidn wean diamoi in dea Richtung ausglegt, dass d´Heh vo da Seitnflächn zua Hejftn da Basiskontn im Vahejdnis vom Goidnan Schnidd standad. Agrad de Textstej, de wo do dazuaghean dad, loßt se oba niat eindeitig auslegn. Ondraseits wead aa d´Thesn vatredn, dass as Vahejdnis 2:π fia Pyramidnheh zua Basiskontn de tatsächlichn Moße no bessa wiadaspiaglad. Da Unterschied vo dene zwoa Thesn is 1,0 Promille – oiso ned vui.
Vui Weak aus da griachischn Antikn wean ois Beispui fiad Vawendung vom Goidnan Schnidd ogseng wia d´Vordafront vom 447–432 v. Kr. untam Perikles aufgstejhdn Parthenon-Tempel auf da Athener Akropolis heromad. Iatz hand´ zua dene oba koane Pläne ibaliafad und ma woaß ned, obs de Proportionan duach Zuafoi oda bewusst so gwejhd hom.
Oa in spädane Epochn gibts mehrane Beispui fia goidne Proportionan, wia beispuisweis da Dom vo Florenz, d´Notre Dame in Paris oda d´Torhalle in Lorsch (770 n. Kr.)
Es gibt oba koan empirischn Nochweis fiah a signifikant greßane Haifigkeit vom Goidnan Schnidd in dene Epochn ois wia bei ondane Teilungsvahejdnisse. Ebenso fejhn historische Beleg´ fiah a obsichtliche Vawendung vom Goidnan Schnidd.
Da Architekt und Mola Le Corbusier (1887–1965) hod, basiarend auf de menschlichn Moßn und am Goidnan Schnidd, ab 1940 a eiheitlichs Moßsystem entwicklt. In seina Schrift Der Modulor (1949), de wo zu de bedeitendstn Schriftn vo da Architektuagtheorie ghead, hoda des vaeffntlicht. Scho 1934 is eahm fiad Owendung vo mathematischn Ordnungsprinzipien vo da Universitet Zürich da Titl doctor honoris causa vo de mathematischn Wissnschoftn valiahn worn.
Kunst[Werkeln | Am Gwëntext werkeln]
Inwiaweid d´Vawendung vom Goidnan Schnitt in da Kunst za bsundas ästehtische Ergniss fiaht, is letztlich a Frog vo da jeweis herrschadn Kunstauffossung. Fiah d´generelle Thesn, dass de Proportion bsundas osprechad und harmonisch empfundn wead, gibts koane gschichtlichn Belege. Vui Kinstla setztnd an Goidnan Schnitt bewusst ei, bei vui Weakn hand d´Kunsthistoriker eascht im Nochhinein drauf gstoßn. De Befund han olladings ongsichts vo de Haufa an Kandidaten fian Goidnan Schnitt, wia mas in am reich vaziahdn Gmejdt´ findn ko, oft umstrittn.
So wean an Haufa Skuiptuan vo griachischn Buidhauan, wia beispuisweis de Skuiptua Apollo von Belvedere, de wo am Leochares (uma 325 v. Kr.) zuagschrim wead, oda de Weake vo Phidias (5. Jhd. v. Kr.) ois Beispui fiad Verwendung vom Goidnan Schnitt ogseng. Aufn letztan beziagt se aa de heid ibliche Bezoachnung Φ fia an Goidnan Schnitt, de wo vom amerikanischn Mathematiker Mark Barr eigfiaht worn is. De emfois vawendte Bezoachnung τ beziagt se dagegn aufs griachische Woat tome fia Schnitt.
Da Goidne Schnitt werd aa in fui Gmejdter da Renaissance vermuat´, wia bei Raffael, Leonardo da Vinci und Albrecht Dürer, zum Beispui bei Dürers Sejbstbuidnis 1500 und seim Kupferstich Melancolia I vo 1514.
Kinstla vo da Neizeid, de an Goidnan Schnitt bewusst eisetztand han beispuisweis Mondrian, Paul Signac und Georges Seurat, Herge odraa de Kinstla vo da Section d'Or.
Aa in da Fotografie werd da Goidne Schnitt zua Buidgstaltung eigsetzt, wia beispuisweis vom franzäsischn Fotograf Henri Cartier-Bresson.
Im Buachdruck is friahras gelegentlich d´Nutzflächn vo a Seitn, da sognennde Satzspiegel, so positioniert, dass as Vahejdnis vom Bundsteg zum Kopfsteg zum Außensteg zum Fuaßsteg se wia 2:3:5:8 vahoidt. De Wahl wo dene Fibonacci-Zoin approximiert an Goidnen Schnitt.
Künstla und Hondwerka ham im 19. Joarhundert zua Konstruktion beziahungsweis zua Überprüfung vom Goidnen Schnitt oft aa an Goidnen Zirkel hergnumma, dem wo seine beide Schenkel x-förmig noch ohmad zua am zwoatn Zirkel verlängert gwehn hand´, und dem seine Schenkellängen so gwejhd warn, dass as Vahejdnis da beidn Obschnitt´ an Goidnen Schnitt buidt hod. Andane Instrumenter ham d´Form von am Storchschnabel ghabt.
Literatua[Werkeln | Am Gwëntext werkeln]
Historische Literatua[Werkeln | Am Gwëntext werkeln]
- Martin Ohm: Lehrbuch der gesammten höhern Mathematik. Bd 2. Friedrich Volckmar, Leipzig 1835, 1837. (weniger abstrakt, mehr anschaulich)
- Adolf Zeising: Neue Lehre von den Proportionen des menschlichen Körpers. Leipzig 1854.
- Adolf Zeising: Das Normalverhältniss der chemischen und morphologischen Proportionen. Rudolph Weigel, Leipzig 1856.
- Gustav Theodor Fechner: Zur experimentalen Ästhetik., Hirzel, Leipzig 1871. (Vorschule der Ästhetik)
Neiare Literatua[Werkeln | Am Gwëntext werkeln]
- Hans Walser: Der Goldene Schnitt. Edition am Gutenbergplatz, Leipzig 2004. ISBN 3-937219-00-5 (anschaulich geschriebenes Standardwerk des Basler Mathematikers)
- Dr. Ruben Stelzner: Der goldene Schnitt und das Mysterium der Schönheit. in: Tycho de Brahe Jahrbuch. Tycho-Brahe-Verl., Niefern-Öschelbronn 2005. ISBN 3-926347-28-7 (naturwissenschaftlich-philosophische Darstellung)
- P. H. Richter, H.-J. Scholz: Der Goldene Schnitt in der Natur. in: Ordnung aus dem Chaos. Hrsg. B.-O. Küppers. Serie Piper. Piper, München 1987, S. 175–214. ISBN 3-492-10743-5
- Hans Walser: Der Goldene Schnitt. Teubner, Stuttgart 1993. ISBN 3-8154-2511-5, ISBN 3-7281-2336-6
- Marguerite Neveux, H. E Huntley: Le nombre d’or – Radiographie d’un mythe. Seuil, Paris 1995. ISBN 2-02-025916-8
- Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum Akad. Verl., Heidelberg, Berlin – Oxford ²1996. ISBN 3-86025-404-9
- Roger Herz-Fischler: A mathematical History of the Golden Ratio. Dover Publications, New York 1998. ISBN 0-486-40007-7
- Jürgen Fredel: Maßästhetik. Studien zu Proportionsfragen und zum Goldenen Schnitt. Lit Verlag, Hamburg 1998. ISBN 3-8258-3408-5 (Diss. Hamburg, 1993)
- Thomas Koshy: Fibonacci and Lucas Numbers with Applications. John Wiley & Sons, New York 2001, S. 239–299. ISBN 0-471-39969-8
- Albert van der Schoot: Die Geschichte des goldenen Schnitts. Frommann-Holzboog, Stuttgart – Bad Cannstatt 2005. ISBN 3-7728-2218-5
- S. King u. a.: On the mystery of the golden angle in phyllotaxis. in: Plant, cell & environment (PC & E). Blackwell, Oxford 27.2004,6 (Juni), S. 685–96.
- Klaus Podirsky: Fremdkörper Erde – Goldener Schnitt und Fibonacci-Folge und die Strukturbildung im Sonnensystem. Kontext. info3-Verlag 2004. ISBN 3-924391-29-7 (Die faszinierende These einer gemeinsamen Evolution von Kosmos, Erde und Mensch)
- Hrant Arakelian. Mathematics and History of the Golden Section, Logos 2014, 404 p. ISBN 978-5-98704-663-0 (rus.).
- Nautilus, the enigma of the empire, Osvaldo Rea, ISBN 88-901473-8-5
- Nautilus, l'enigma dell'impero, Osvaldo Rea, ISBN 88-901473-9-3
- Nautilus, l'enigme de l'empire, Osvaldo Rea, ISBN 88-901473-7-7
Im Netz[Werkeln | Am Gwëntext werkeln]
- Marcus Frings: Der Goldene Schnitt (kritische Analyse)
- Marcus Frings: The Golden Section in Architectural Theory (kritische Analyse)
- Ruben Stelzner: Der Goldene Schnitt und das Mysterium der Schönheit, (2002)
- Der Goldene Schnitt in der Biologie (englisch)
- Bilder zum Goldenen Schnitt in der Biologie
- Der Goldene Schnitt unter Einbeziehung von Beispielen aus Kunst, Architektur und der menschlichen Anatomie
- Bernhard Peter: Goldener Schnitt – Mathematik und Bedeutung in der Kunst (insbes. 34 verschiedene Konstruktionverfahren)
- "Höhere Pflanzen-Mathematik"
- Kleine Abhandlung über Spiralen, Fibonacci-Zahlen und den Goldenen Schnitt (mit Onlineberechnung)
- Projekt am Kaiser-Heinrich-Gymnasium Bamberg
- Ausführliche und gut lesbare Darstellung des Goldenen Schnittes und der Fibonacci-Zahlen (englisch)
- DIN-Papier und Goldener Schnitt
- Eine Theorie über die Rolle des Goldenen Schnitts bei der Informationsverarbeitung im Gehirn
- Facharbeit zum Thema "Klangspektrenvergleiche basierend auf der Fourier-Analyse. Versuch der Synthese eines "Goldenen Klangs"."
- Historische Beispiele und einfache Herleitungen zum Goldenen Schnitt
- Ein Tool zum Berechnen des Goldenen Schnitts
Dea Artike is ois zimfti in de Hall of Fame (Ruhmeshoin) aufgnumma worn.
|



![{\displaystyle \Phi ={\frac {a}{b}}={\frac {1+{\sqrt {5}}}{2}}=e^{-0.2i\pi }+e^{0.2i\pi }=e^{-0.2\ln -1}+e^{0.2\ln -1}=-1^{-0.2}+-1^{0.2}={\frac {1}{\sqrt[{5}]{-1}}}+{\sqrt[{5}]{-1}}=1{,}618033988{...}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc78913f7fb1e123cc6c090f34cac33981b7e82f)








