Sejbstähnlichkeit
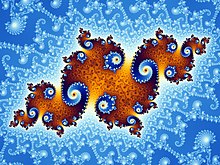
Sejbstähnlichkeit im engan Sinn is de Eignschaft vo Gegnständn, Kerpan, Mengen oda geometrischn Objektn, in gressan Maßstobm, d. h. bei Vagressarung desejm oda ähnliche Strukturn aufzweisn wia im Ofangszuastand. De Eignschaft werd unta andam vo da fraktaln Geometrie untasuacht, wei fraktale Objekte a hohe bzw. perfekte Sejbstähnlichkeit aufweisn. De Mandlbrotmenge is streng gnumma und im Gegnsotz zu oft vortroganan Moanunga ned sejbstähnli: Im Prinzip ko ma jedn Ausschnitt vom Rand in jeda Vagressarung bei ausreichenda Auflesung osegn, vo wejchan Punkt a stammt.
Im weidan Sinn werd da Begriff aa in da Philosophie und in de Sozial- und Naturwissnschaftn vawendt, um grundsätzle wiedakehrende, in si sejm vaschochtlte Strukturn z bezeichna.
Fraktale Geometrie
[Werkeln | Am Gwëntext werkeln]
Vo ana exaktn (oda 'striktn) Sejbstähnlichkeit is de Rede, wenn bei unendlicha Vagressarung vom untasuachtn Objekt imma wieda de urspringliche Struktur dahoidn werd, ohne jemois a elementare Feinstruktur zum dahoitn.
Exakte Sejbstähnlichkeit is praktisch nur bei mathematisch (z. B. durch a iterierts Funktionen-System) erzeigtn Objektn z findn. Beispui dafia san s Sierpinski-Dreieck, Koch-Kurvn, de Cantor-Menge oda trivialaweis a Punkt und a Gerade.
De Mandelbrot-Menge und de Julia-Menge san sejbstähnlich, ned oba strikt sejbstähnlich. Strikte Sejbstähnlichkeit impliziert Skaleninvarianz und losst sich unta andam mit Huif vo de charakteristischn Exponentn vom zgrundliegendn Potenzgesetz (Skalengesetz) quantifiziern.
Natur
[Werkeln | Am Gwëntext werkeln]
Real existiarende Beispui waradn z. B. de Vaastelung von Bluatgefäßn, Farnbladdln oda Tei vo am Blumenkoi (Romanesco). Bei ana Vagressarung schaugt a Stickal wia a ganza Blumenkopf aus. Bei realen Beispuin losst si de Vagressarung oba ned bis ins Unendliche weita furtsetztn, so wia bei idealn Objektn aus da fraktalen Geometrie.
Bei realen Beispielen lässt sich die Vergrößerung selbstverständlich nicht bis ins Unendliche fortsetzen, wie es bei idealen Objekten der Fall wäre.
De Sejbstähnlichkeit is a Phänomen, des wo oft in da Natur auftritt. A kennzeichnende Zoi fia de imma wiedakehrende Sejbstähnlichkeit is da Goidane Schnitt.
Beispuia
[Werkeln | Am Gwëntext werkeln]Fibonacci-Kettn
[Werkeln | Am Gwëntext werkeln]Mia ku mid zwou Regln a ganz oafache Buachstoomfoign macha wo sejbsteendlich is:
a) fang oo mid "k"
b) dausch an-jäds "k" mid an "l" und an-jäds "l" mid an "lk" aus
Oiso:
1. k
2. l
3. lk
4. lkl
5. lkllk
6. lkllklkl
7. lkllklkllkllk
8. lkllklkllkllklkllklkl
...
Mia sichd aa, das mia aagraadd de sejbe Foign macha ku wemma mid
1. k
und
2. l
ofangd und aft in jedä naaxdn Zejn de lezde und de ander hintarananda hĩschreibt:
3. lk
4. lkl
5. lkllk
...
Iadz ku ma si zwoa Zejn aussasuacha, de wo glei hintarananda kemman, zB. de 6. und de 7. und wemma de iadz " k' " und " l' " hoassd, dann is glar, das de 8. Zejn oafach " l'k' " sej muas. Mia sichd oiso das de ganze Fojgn in dem Sinn sejbsteendlich is. De Abfolge " lk " kimmt auf jäda Hierarchi ojwei wida fia und dees obwoj de Fojgn ned periodisch is. De Buachstoom-Fojng hoassd si Fibonacci-Kette.
trivials Beispui
[Werkeln | Am Gwëntext werkeln]Wenn a Kettn periodisch is:
lklklklklklklklklklklk ...
iss nadiale aa sejbsteendlich.
Literatua
[Werkeln | Am Gwëntext werkeln]- Henning Fernau: Iterierte Funktionen, Sprachen und Fraktale, B. I. Wissenschaftsverlag, Mannheim - Wean - Zürich 1994.
Im Netz
[Werkeln | Am Gwëntext werkeln]| → Dea Artikl basiad auf ara frein Ibasetzung vom säim Artike in da Wikipedia af deitsch. |
